銅パターンに流れる電流をVBAでシミュレーションする

2021年2月2日2023年1月21日

目次 [ close ]

お手軽に電流の流れ方をシミュレーションしたい

基板設計では、「どのようなパターン形状が適切か」を事前に検討したいものです。しかし、電流分布をシミュレーションできるソフトウェアは一般に高価です。個人での購入などもっての外、会社でも面倒な手続きが必要になる価格帯であることもしばしば。

そこで、ほとんどのPCで使うことのできるExcel VBAを使って、電流分布のシミュレーションができるプログラムを作ってみました。

Excelを選んだ最大の理由は、何より特別な実行環境が不用であることです。多くの職場・個人PCにはExcelがインストールされています。最終的にはウェブブラウザでアクセスさえすれば使えるシミュレータを作りたいところですが、まずは足がかりとしてExcel VBAで実現してみます。

目指すもの

電流の流れ方を計算するためには、最低限パターンの形状と、電流源（ソース）・電流吸い込み点（シンク）の位置を入力する必要があります。これらをエクセルのセル上に表現し、ヒートマップで電流密度を表現できるものを目指します。

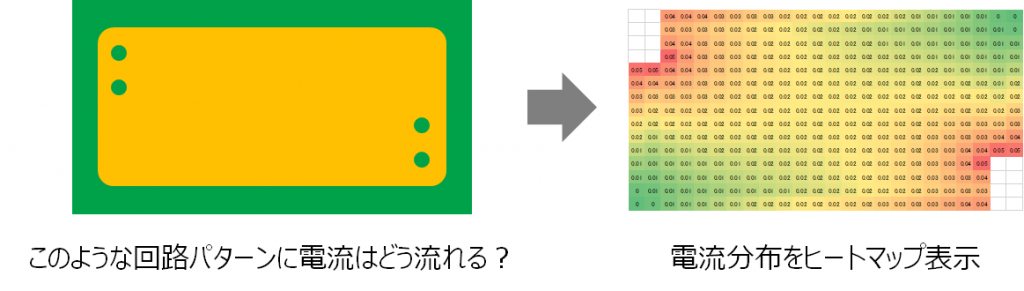
なお、なるべく簡単な計算で実現するため、電流の絶対値を求めるのではなくパターンに流れる電流密度の比を求めることに留めます。

シミュレーションの考え方

①回路パターンをコンピュータで計算できる形にするため、②セルに離散化します。まずは③電圧分布を計算し、その後に④電流分布を計算します。ここでは、③電圧分布を電圧マップ、④電流分布を電流マップと呼ぶこととします。

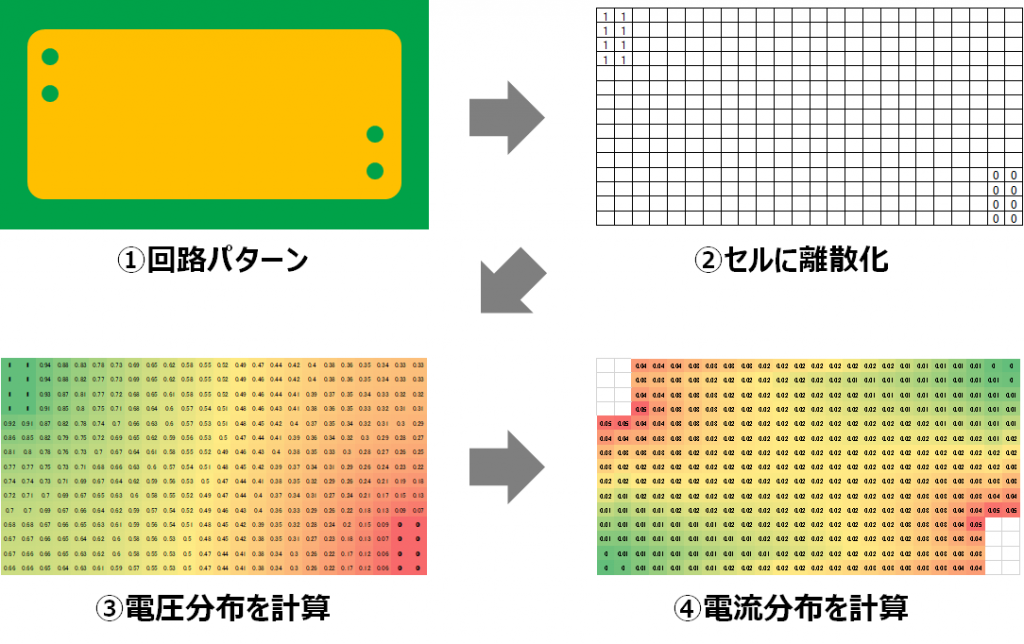
パターンを離散化するためには、パターンを何らかの回路に置き換えて計算する必要があります。今回はメッシュ抵抗（抵抗器を格子状に接続した回路）に置き換えて、コンピュータで計算できる形に変換します。（抵抗はすべて同じ値である前提です）
Excelのセルは回路の接続点の電圧を示し、それぞれのセルが抵抗器で接続されているイメージです。

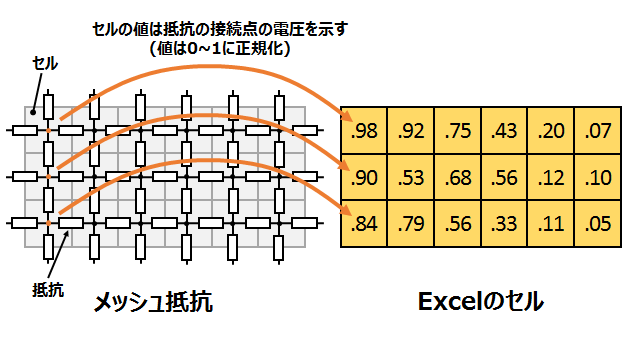
ちなみに、このようにモデルを格子状に区切って計算するシミュレーション手法を格子法と呼びます。

計算の流れ

まず、簡単のため一本の配線で考えてみます。
ここでは電圧・電流を正規化して、ソース部（電流供給点）の電圧を1、シンク部（電流吸い込み点）の電圧を0として計算します。すなわち、ソース部は電源供給部、シンク部はICの電源ピンや負荷を指します。

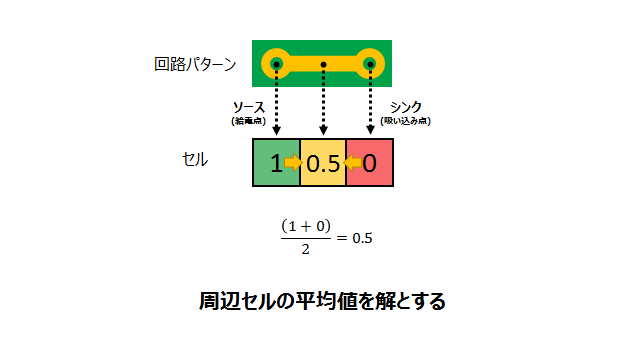
電流源となるソース、電流が吸い込まれるシンク、電流値を求めたい配線のセルを定義します。上で述べたように、電流をはじめから求めることはできないので、まずは電圧分布を求めます。

計算対象の配線セルは隣接するセルの電圧を平均して求めるので、左の電流ソースの電圧”1”と、電流シンクの電圧”0”を平均します。1と0の平均なので、配線部の電圧は0.5となります。

これを二次元に拡張してみます。四方が囲まれたセルであれば同様に計算できますね。

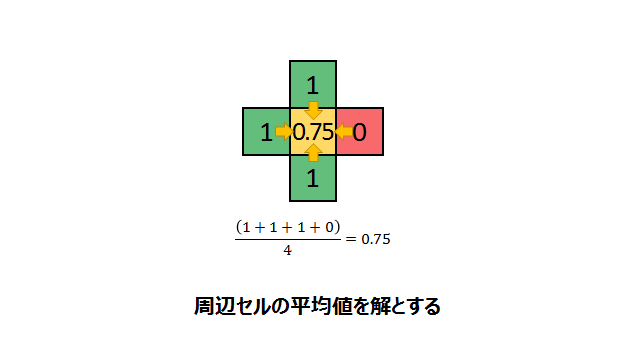
先ほどの例では配線セルに隣接するセルはすべて既知の値だったので、これを平均化するだけで求められました。しかし、ソースとシンクの間に複数のセルがある場合はどうでしょうか。隣接するセルもまた、未知のセル（計算対象のセル）です。

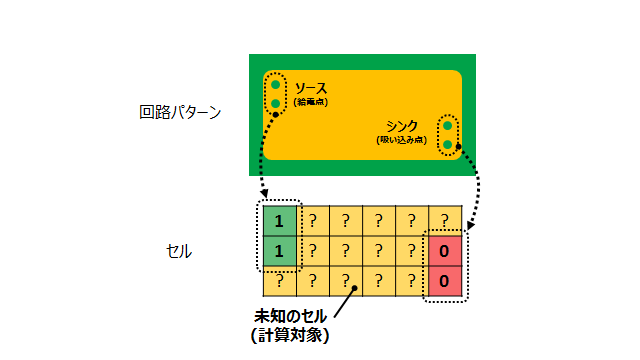
このような場合、はじめに何らかの初期値を入れておき、何度も繰り返し計算することで相互に隣接セルと相互に影響を与え、段々と値を収束させることで解を求めます。下記の例では、初期値として未知のセル（黄色のセル）に0を入れています。

ループ演算を繰り返していくに従い、段々と値の変化が小さくなってゆきます。下記の例では、10回程度のループ演算でほぼ値に変化がなくなりました。

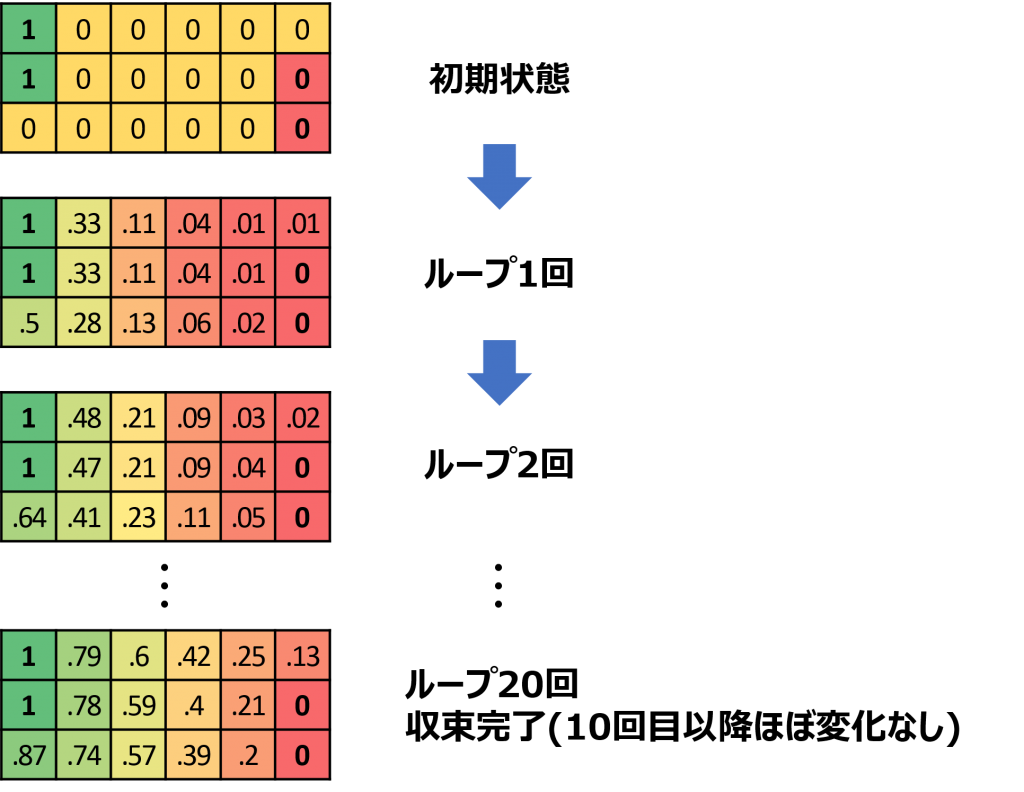
収束したか否かは、計算前後での値の変化が一定値より小さくなったかで判定します。詳しくは「収束の評価」の章をご覧ください。

Excel VBAでのプログラム

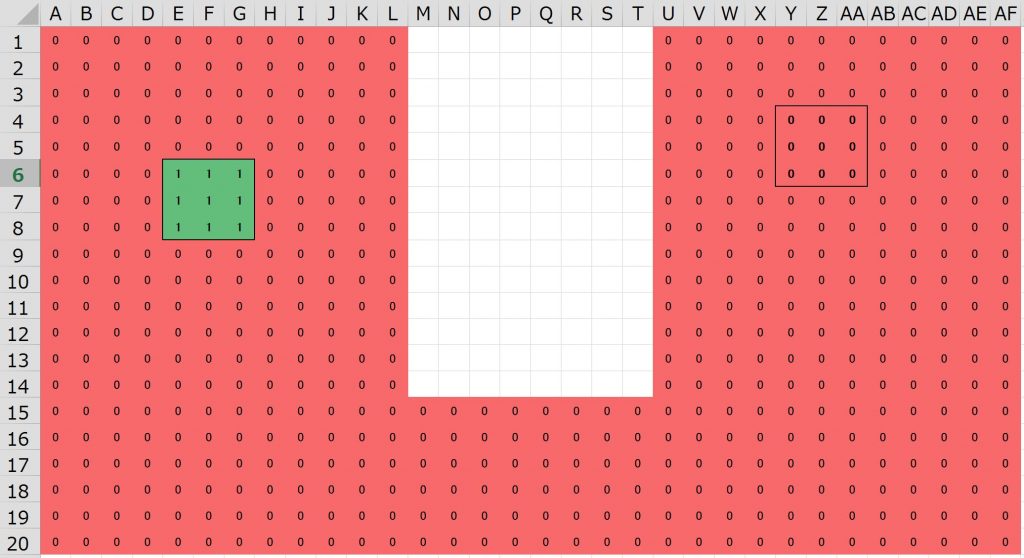
凹型の回路パターンをExcelのシートで作成しました。ソース部からシンク部に電流が流れるのであれば、M~T列の細いパターンに電流が集中するはずです。

初期状態

緑のセルがソース（給電点）、赤（太字の0）のセルがシンク（吸い込み点）で、その他のセルは配線セルですが、初期値として0を入れています。パターンサイズはH：20(縦)×W：32(横)です。

電圧マップの演算

これは電流マップのループ演算で値が変化していく様子をGIFアニメにしたものです。電流ソースと電流シンクが影響し合っている様子がわかります。

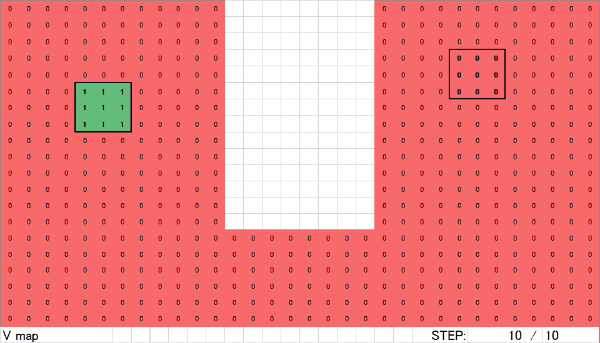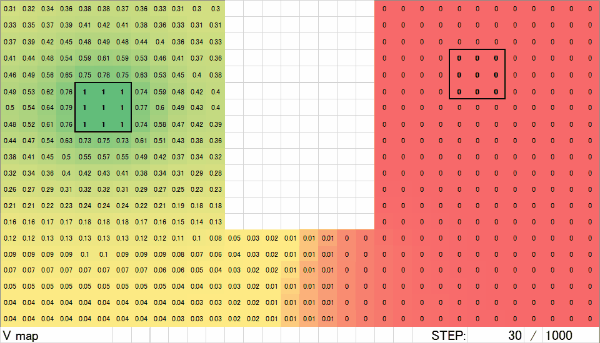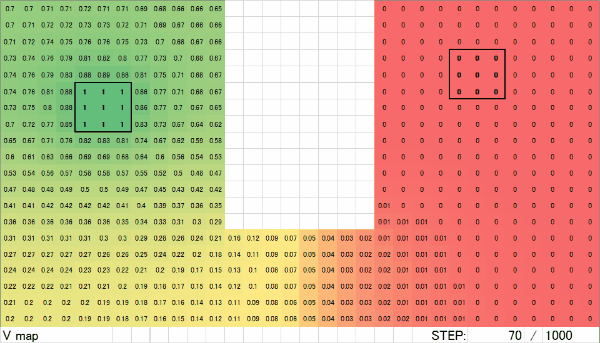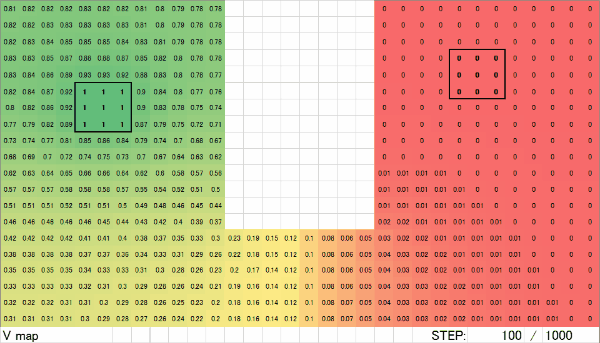
1000ループ完了後の電圧マップです。電流ソース(1)と電流シンク(0)の間がグラデーションしています。M列～T列に着目してみると、他の場所に比べて数値の変化が大きくなっています。これは、パターンが細くなっている部分で電圧降下が大きくなることを示しています。

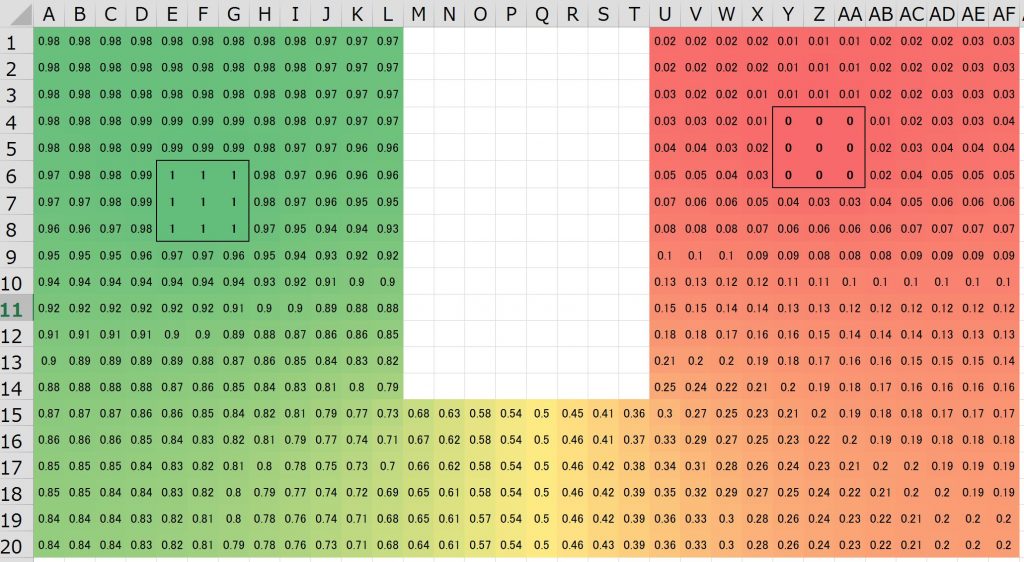
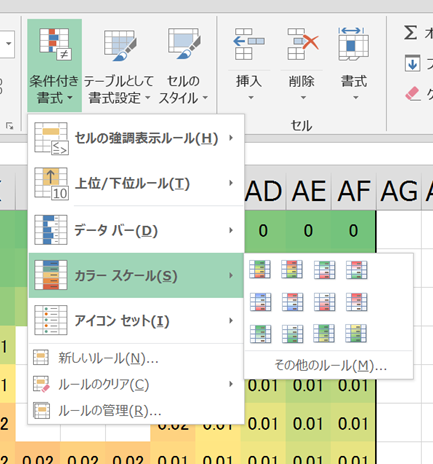
なお、セルには条件付き書式（カラースケール）を設定することでヒートマップ表示しています。

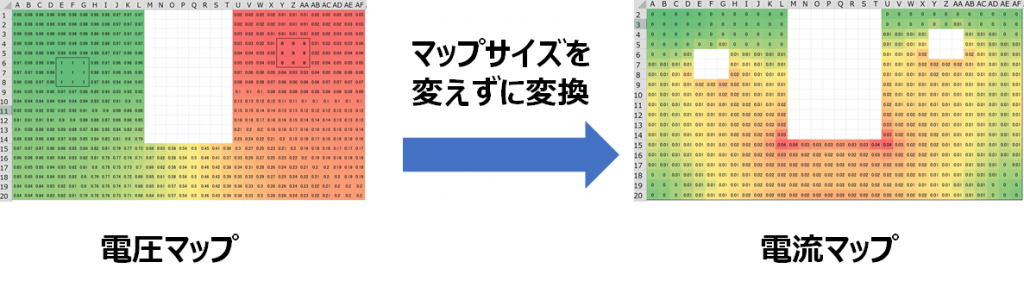
電圧マップから電流マップへの変換

電圧マップが確定したので、最後に電流マップへ変換します。電圧から電流を求めるにはオームの法則V=RIより、電圧マップの値を抵抗値で割る必要があります。しかし、このヒートマップにおいて抵抗値は常に一定であるため、電位差をそのまま電流の比として扱うことができます。

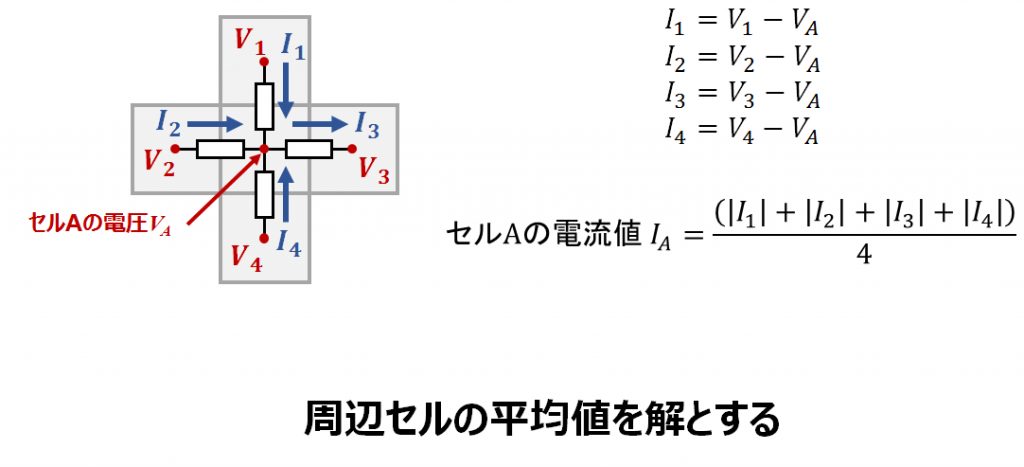
ただし、元のマップは横幅Wセル×高さHセルで構成されています。単にセル間の電圧差を求めても、W×Hのマップになりません。そこで、計算対象のセルに流入・流出する電流の平均値を計算対象セルの電流値とすることにします。四方から流入・流出する電流はそれぞれ計算対象のセルAと、周辺セルの電圧差を取れば求まります。

電流の方向は考慮していないため、絶対値を取り、平均してセルAの電流値とします。

上記のアルゴリズムにより生成した電流マップをGIFアニメにしました。

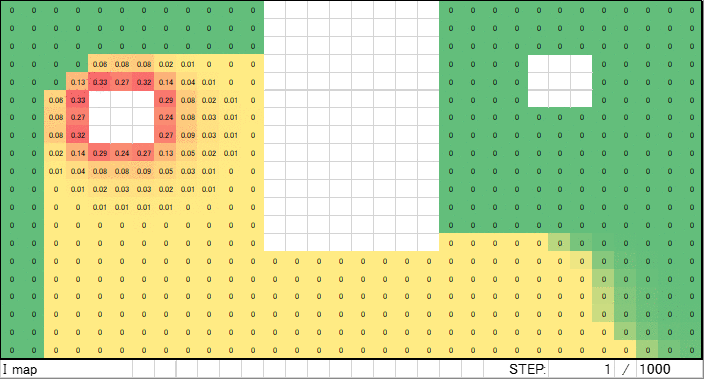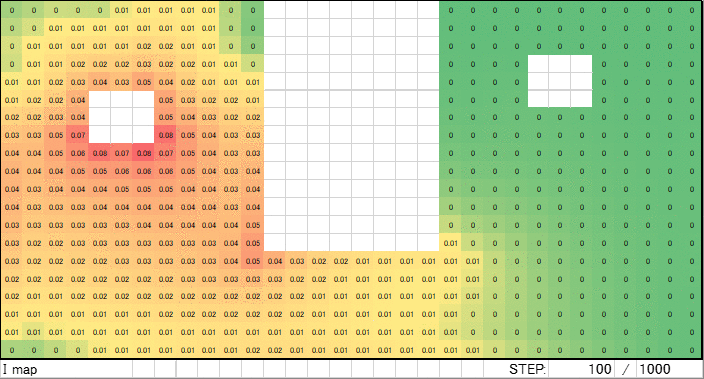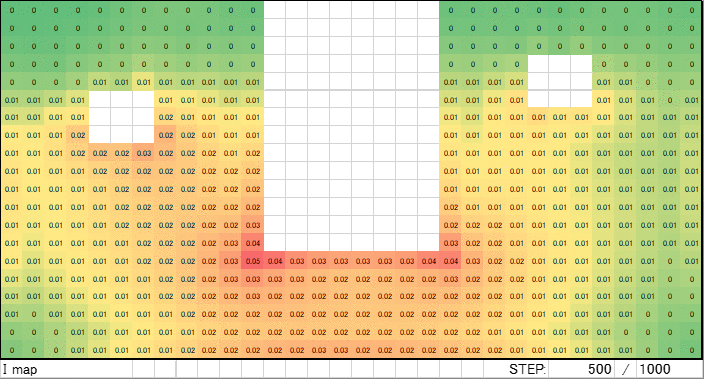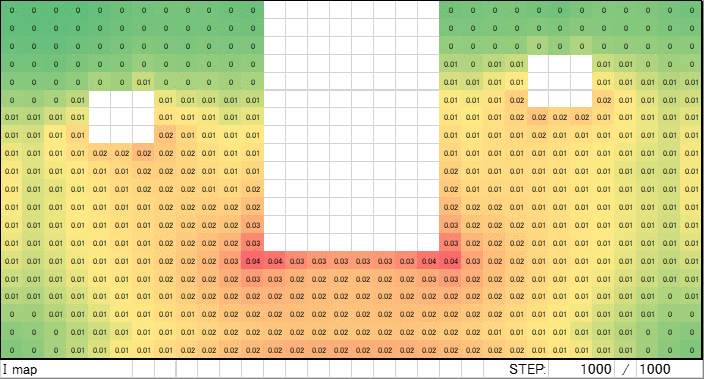
1000ループ完了後の電流マップがこちらです。電流ソースと電流シンクを結ぶ最短ルート上のセルが赤くなりました。おおよそ期待する結果と一致するデータが得られました。

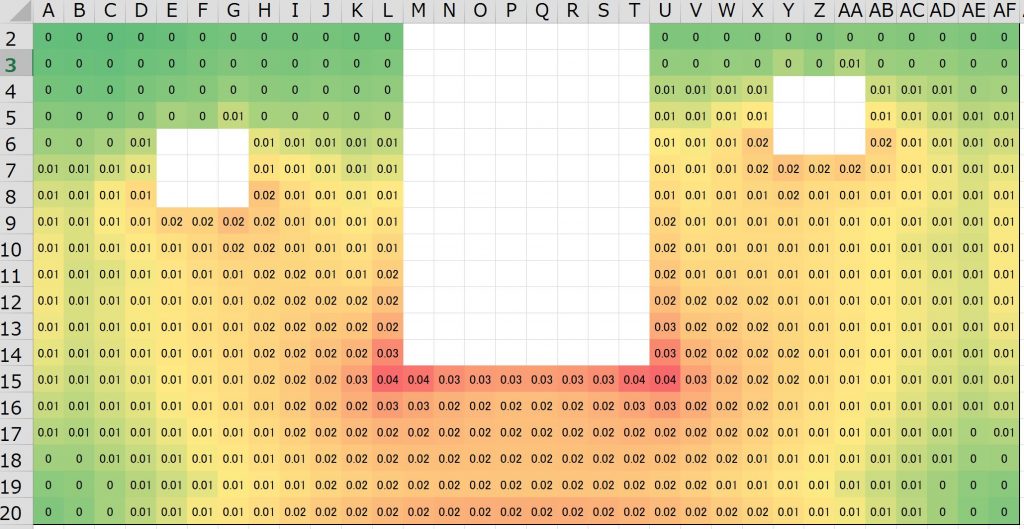
計算結果の評価

直感的にはそれっぽいデータが得られましたが、これが正しい結果であることを確かめなければ設計に役立てることはできません。

正気の沙汰とは思えませんが、LTspiceで上記と同様のの32×20グリッド抵抗を再現しました。左側が電圧源、右側がグランドです。この回路網でシミュレーションを実行し、抵抗に流れている電流をExcelでの結果と比較します。

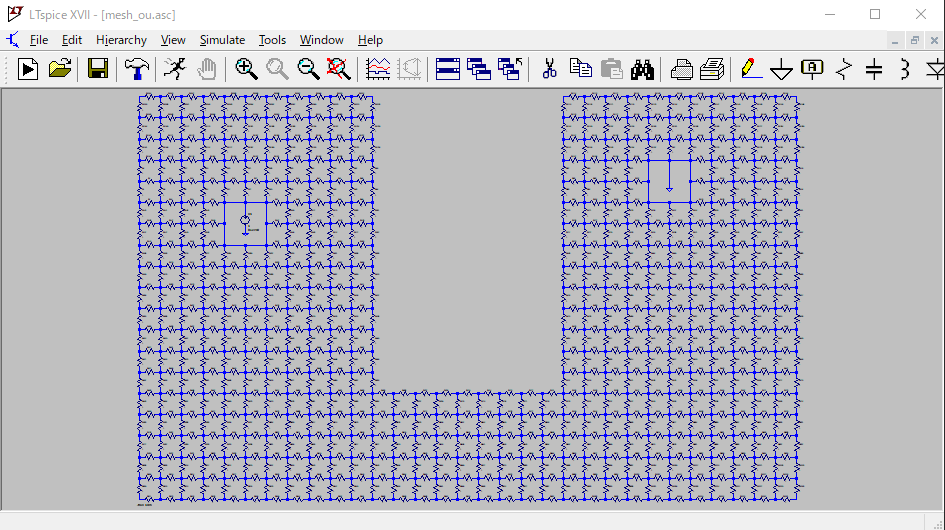
LTspiceでは電圧をヒートマップ表示することはできませんが、プローブをあててピンポイントで電圧や電流を観測することができます。下記は一例ですが、VBAでも大きく変わらない値が得られていることが確認できました。

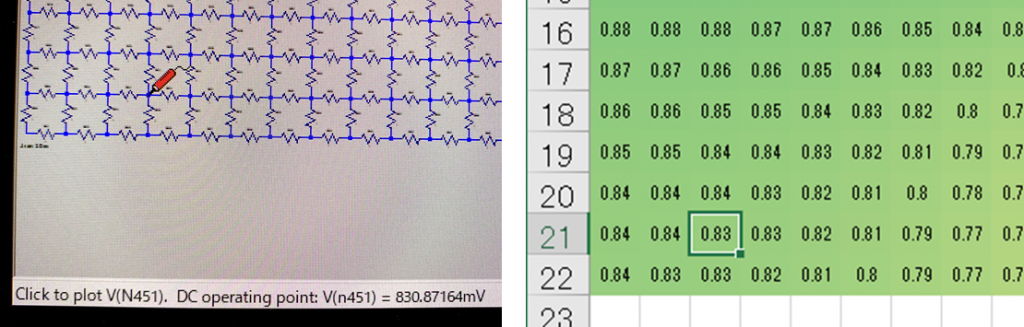
収束の評価

収束するまでのループ回数は、パターンの形状や電流ドレーン・電流シンクの位置関係で変化してしまいます。手動で収束の判定をしてもよいですが、せっかくなのでしきい値も自動決定できるものを今後目指していきたいと思います。

収束の判定は、演算前後でのマップ同士のユークリッド距離で評価することにしました。ユークリッド距離とは、多次元ベクトルどうしの幾何的な距離（違い）を定量的に表現する手法です。画像処理の分野でよく使われる手法です。

電圧マップ演算のループごとにユークリッド距離を計算し、値が一定値以下になれば収束したとみなすことにします。

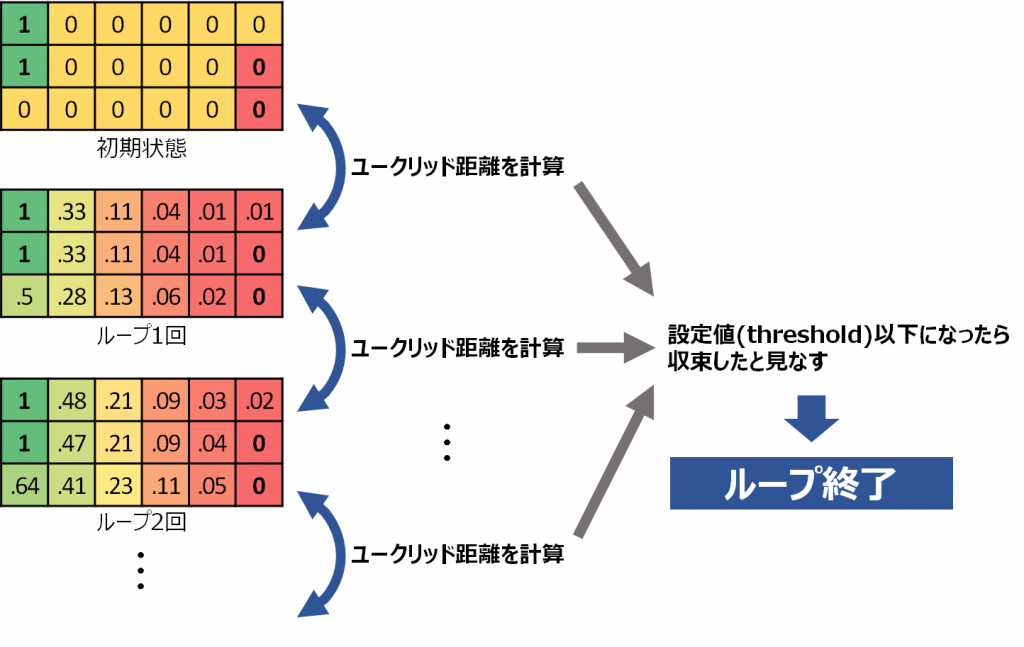
スレッショルド（しきい値）の設定

では、事前に設定するスレッショルドはどのように決めればよいのでしょうか。ループ回数が多ければ多いほど結果は正確になりますが、「結果は収束する」ことを前提とすれば、「変化が一定以下になれば計算が完了した」と判断することができます。

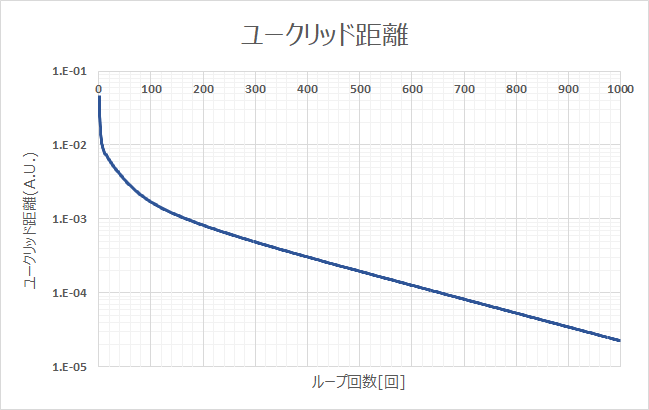
ループ回数1000回で計算したユークリッド距離の変化を下記のグラフに示します。グラフでは300回時点で収束しているように見えますが、実際の300回時点の電流マップでは700～800回程度で変化しなくなったように見えました。つまり、対数スケールで直線になったからと言って、電流マップ上の値が収束したとは限らないようです。